Returns the least common multiple between two integer values. : Math « Development Class « Java

1. Java
2. Development Class
3. Math

Returns the least common multiple between two integer values.

       
import java.io.File;

/* 
 * Licensed to the Apache Software Foundation (ASF) under one or more
 *  contributor license agreements.  See the NOTICE file distributed with
 *  this work for additional information regarding copyright ownership.
 *  The ASF licenses this file to You under the Apache License, Version 2.0
 *  (the "License"); you may not use this file except in compliance with
 *  the License.  You may obtain a copy of the License at
 *
 *      http://www.apache.org/licenses/LICENSE-2.0
 *
 *  Unless required by applicable law or agreed to in writing, software
 *  distributed under the License is distributed on an "AS IS" BASIS,
 *  WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
 *  See the License for the specific language governing permissions and
 *  limitations under the License.
 *
 *
 */
public class Main {

  /**
   * Returns the least common multiple between two integer values.
   * 
   * @param a the first integer value.
   * @param b the second integer value.
   * @return the least common multiple between a and b.
   * @throws ArithmeticException if the lcm is too large to store as an int
   * @since 1.1
   */
  public static int lcm(int a, int b) {
      return Math.abs(mulAndCheck(a / gcd(a, b), b));
  }
  /**
   * Multiply two integers, checking for overflow.
   * 
   * @param x a factor
   * @param y a factor
   * @return the product <code>x*y</code>
   * @throws ArithmeticException if the result can not be represented as an
   *         int
   * @since 1.1
   */
  public static int mulAndCheck(int x, int y) {
      long m = ((long)x) * ((long)y);
      if (m < Integer.MIN_VALUE || m > Integer.MAX_VALUE) {
          throw new ArithmeticException("overflow: mul");
      }
      return (int)m;
  }

  /**
   * <p>
   * Gets the greatest common divisor of the absolute value of two numbers,
   * using the "binary gcd" method which avoids division and modulo
   * operations. See Knuth 4.5.2 algorithm B. This algorithm is due to Josef
   * Stein (1961).
   * </p>
   * 
   * @param u a non-zero number
   * @param v a non-zero number
   * @return the greatest common divisor, never zero
   * @since 1.1
   */
  public static int gcd(int u, int v) {
      if (u * v == 0) {
          return (Math.abs(u) + Math.abs(v));
      }
      // keep u and v negative, as negative integers range down to
      // -2^31, while positive numbers can only be as large as 2^31-1
      // (i.e. we can't necessarily negate a negative number without
      // overflow)
      /* assert u!=0 && v!=0; */
      if (u > 0) {
          u = -u;
      } // make u negative
      if (v > 0) {
          v = -v;
      } // make v negative
      // B1. [Find power of 2]
      int k = 0;
      while ((u & 1) == 0 && (v & 1) == 0 && k < 31) { // while u and v are
                                                          // both even...
          u /= 2;
          v /= 2;
          k++; // cast out twos.
      }
      if (k == 31) {
          throw new ArithmeticException("overflow: gcd is 2^31");
      }
      // B2. Initialize: u and v have been divided by 2^k and at least
      // one is odd.
      int t = ((u & 1) == 1) ? v : -(u / 2)/* B3 */;
      // t negative: u was odd, v may be even (t replaces v)
      // t positive: u was even, v is odd (t replaces u)
      do {
          /* assert u<0 && v<0; */
          // B4/B3: cast out twos from t.
          while ((t & 1) == 0) { // while t is even..
              t /= 2; // cast out twos
          }
          // B5 [reset max(u,v)]
          if (t > 0) {
              u = -t;
          } else {
              v = t;
          }
          // B6/B3. at this point both u and v should be odd.
          t = (v - u) / 2;
          // |u| larger: t positive (replace u)
          // |v| larger: t negative (replace v)
      } while (t != 0);
      return -u * (1 << k); // gcd is u*2^k
  }
}

   
    
    
    
    
    
    
  

Related examples in the same category

1.	Absolute value
2.	Find absolute value of float, int, double and long using Math.abs
3.	Find ceiling value of a number using Math.ceil
4.	Find exponential value of a number using Math.exp
5.	Find floor value of a number using Math.floor
6.	Find minimum of two numbers using Math.min
7.	Find power using Math.pow
8.	Find square root of a number using Math.sqrt
9.	Find natural logarithm value of a number using Math.log
10.	Find maximum of two numbers using Math.max
11.	Get the power value
12.	Using the Math Trig Methods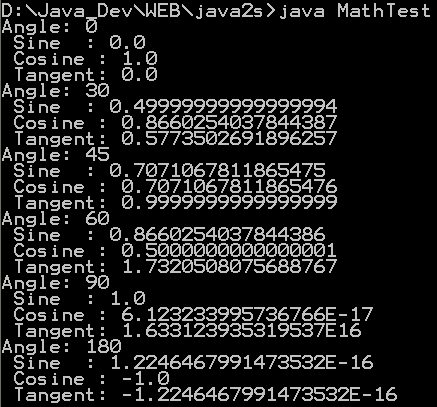
13.	Using BigDecimal for Precision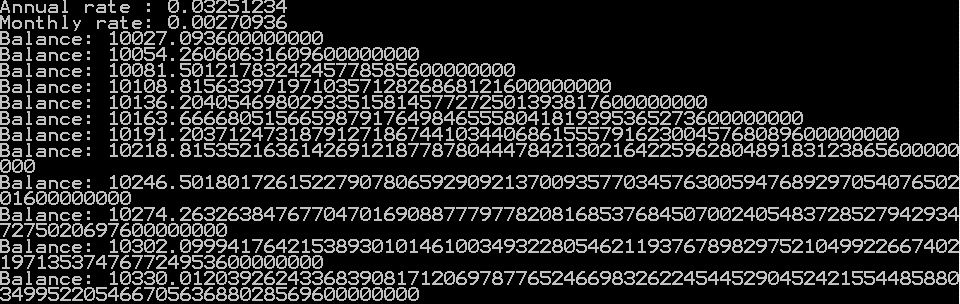
14.	Demonstrate our own version round()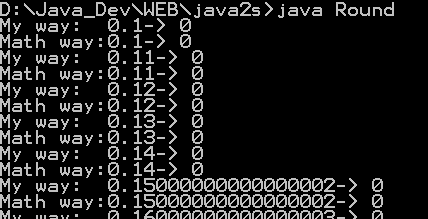
15.	Demonstrate a few of the Math functions for Trigonometry
16.	Exponential Demo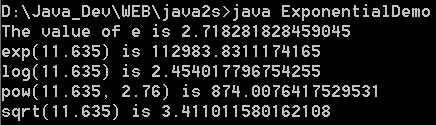
17.	Min Demo
18.	Basic Math Demo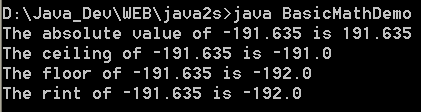
19.	Using strict math in applications
20.	Conversion between polar and rectangular coordinates
21.	Using the pow() function
22.	Using strict math at the method level
23.	Calculating hyperbolic functions
24.	Calculating trigonometric functions
25.	Weighted floating-point comparisons
26.	Solving right triangles
27.	Applying the quadratic formula
28.	Calculate the floor of the log, base 2
29.	Greatest Common Divisor (GCD) of positive integer numbers
30.	Least Common Multiple (LCM) of two strictly positive integer numbers
31.	Moving Average
32.	Make Exponention
33.	Caclulate the factorial of N
34.	Trigonometric Demo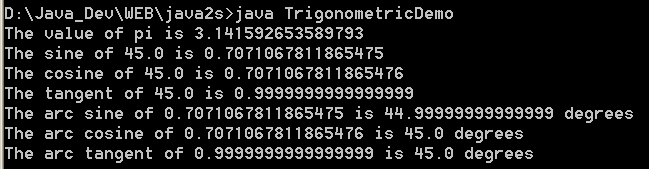
35.	Complex Number Demo
36.	sqrt(a^2 + b^2) without under/overflow
37.	Returns an integer hash code representing the given double array value.
38.	Returns an integer hash code representing the given double value.
39.	Returns n!. Shorthand for n Factorial, the product of the numbers 1,...,n as a double.
40.	Returns n!. Shorthand for n Factorial, the product of the numbers 1,...,n.
41.	Returns the hyperbolic sine of x.
42.	Contains static definition for matrix math methods.
43.	For a double precision value x, this method returns +1.0 if x >= 0 and -1.0 if x < 0. Returns NaN if x is NaN.
44.	For a float value x, this method returns +1.0F if x >= 0 and -1.0F if x < 0. Returns NaN if x is NaN.
45.	Normalize an angle in a 2&pi wide interval around a center value.
46.	Normalizes an angle to a relative angle.
47.	Normalizes an angle to an absolute angle
48.	Normalizes an angle to be near an absolute angle
49.	Returns the natural logarithm of n!.
50.	Gets the greatest common divisor of the absolute value of two numbers
51.	Matrix manipulation
52.	Returns exact (http://mathworld.wolfram.com/BinomialCoefficient.html) Binomial Coefficient
53.	Returns a double representation of the (http://mathworld.wolfram.com/BinomialCoefficient.html) Binomial Coefficient
54.	Returns the natural log of the (http://mathworld.wolfram.com/BinomialCoefficient.html) Binomial Coefficient
55.	Returns the hyperbolic cosine of x.
56.	Math Utils
57.	Implements the methods which are in the standard J2SE's Math class, but are not in in J2ME's.
58.	Utility methods for mathematical problems.
59.	A math utility class with static methods.
60.	Computes the binomial coefficient "n over k"
61.	Log Gamma
62.	Log Beta
63.	Beta
64.	Gamma
65.	Factorial
66.	Computes p(x;n,p) where x~B(n,p)
67.	Returns the sum of two doubles expressed in log space
68.	sigmod
69.	sigmod rev
70.	Numbers that are closer than this are considered equal
71.	Returns the KL divergence, K(p1 || p2).
72.	Returns the sum of two doubles expressed in log space
73.	Returns the difference of two doubles expressed in log space
74.	Is Prime
75.	Statistical functions on arrays of numbers, namely, the mean, variance, standard deviation, covariance, min and max
76.	This class calculates the Factorial of a numbers passed into the program through command line arguments.
77.	Calculates the Greatest Common Divisor of two numbers passed into the program through command line arguments.
78.	Variance: the square of the standard deviation.
79.	Population Standard Deviation
80.	Returns from a static prime table the least prime that is greater than or equal to a specified value.