A math utility class with static methods.
/*
* LingPipe v. 3.9
* Copyright (C) 2003-2010 Alias-i
*
* This program is licensed under the Alias-i Royalty Free License
* Version 1 WITHOUT ANY WARRANTY, without even the implied warranty of
* MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the Alias-i
* Royalty Free License Version 1 for more details.
*
* You should have received a copy of the Alias-i Royalty Free License
* Version 1 along with this program; if not, visit
* http://alias-i.com/lingpipe/licenses/lingpipe-license-1.txt or contact
* Alias-i, Inc. at 181 North 11th Street, Suite 401, Brooklyn, NY 11211,
* +1 (718) 290-9170.
*/
//package com.aliasi.util;
/**
* A math utility class with static methods.
*
* @author Bob Carpenter
* @version 4.0.0
* @since LingPipe1.0
*/
public class Math {
// forbid instances
private Math() {
/* no instances */
}
/**
* The value of the golden ratio. The golden ratio is defined to
* be the value φ such that:
*
* <blockquote>
* φ = (φ + 1) / φ
* </blockquote>
*
* Note that this is a quadratic equation (multiply both sides by
* φ) with the solution roughly <code>1.61803399</code>.
*
* <p>See the following for a fascinating tour of the properties
* of the golden ratio:
*
* <ul>
* <li><a href="http://mathworld.wolfram.com/GoldenRatio.html"
*>Mathworld: Golden Ratio</a></li>
* </ul>
*/
public static final double GOLDEN_RATIO = (1.0 + java.lang.Math.sqrt(5))/2.0;
/**
* The natural logarithm of 2.
*/
public static final double LN_2 = java.lang.Math.log(2.0);
static final double INV_LN_2 = 1.0/LN_2;
/**
* An array of the Fibonacci sequence up the maximum value
* representable as a long integer. The array is defined as
* follows:
*
* <blockquote><pre>
* FIBONACCI_SEQUENCE[0] = 1
* FIBONACCI_SEQUENCE[1] = 2
* FIBONACCI_SEQUENCE[n+2] = FIBONACCI_SEQUENCE[n+1] + FIBONACCI_SEQUENCE[n]
* </pre></blockquote>
*
* So <code>FIBONACCI_SEQUENCE[0]</code> represents the second
* Fibonacci number in the traditional numbering. The inital entries
* are:
*
* <blockquote><code>
* 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597,
* 2584, ...
* </code></blockquote>
*
* The length of the array is 91, and the largest value is:
*
* <blockquote><code>
* FIBONACCI_SEQUENCE[90] = 7540113804746346429
*
* </code></blockquote>
*
* <P>See the following references for more information on
* the fascinating properties of Fibonacci numbers:
*
* <UL>
* <LI> <a href="http://en.wikipedia.org/wiki/Fibonacci_number">Wikipedia: Fibonacci Number</a>
* <LI> <a href="http://mathworld.wolfram.com/FibonacciNumber.html">Mathworld: Fibonacci Number</a>
*/
public static final long[] FIBONACCI_SEQUENCE = new long[] {
1l,
2l,
3l,
5l,
8l,
13l,
21l,
34l,
55l,
89l,
144l,
233l,
377l,
610l,
987l,
1597l,
2584l,
4181l,
6765l,
10946l,
17711l,
28657l,
46368l,
75025l,
121393l,
196418l,
317811l,
514229l,
832040l,
1346269l,
2178309l,
3524578l,
5702887l,
9227465l,
14930352l,
24157817l,
39088169l,
63245986l,
102334155l,
165580141l,
267914296l,
433494437l,
701408733l,
1134903170l,
1836311903l,
2971215073l,
4807526976l,
7778742049l,
12586269025l,
20365011074l,
32951280099l,
53316291173l,
86267571272l,
139583862445l,
225851433717l,
365435296162l,
591286729879l,
956722026041l,
1548008755920l,
2504730781961l,
4052739537881l,
6557470319842l,
10610209857723l,
17167680177565l,
27777890035288l,
44945570212853l,
72723460248141l,
117669030460994l,
190392490709135l,
308061521170129l,
498454011879264l,
806515533049393l,
1304969544928657l,
2111485077978050l,
3416454622906707l,
5527939700884757l,
8944394323791464l,
14472334024676221l,
23416728348467685l,
37889062373143906l,
61305790721611591l,
99194853094755497l,
160500643816367088l,
259695496911122585l,
420196140727489673l,
679891637638612258l,
1100087778366101931l,
1779979416004714189l,
2880067194370816120l,
4660046610375530309l,
7540113804746346429l
};
/**
* Returns <code>true</code> if the specified number is prime. A
* prime is a positive number greater than <code>1</code> with no
* divisors other than <code>1</code> and itself, thus
* <code>{2,3,5,7,11,13,...}</code>.
*
* @param num Number to test for primality.
* @return <code>true</code> if the specified number is prime.
*/
public static boolean isPrime(int num) {
if (num < 2) return false;
for (int i = 2; i <= num/2; ++i)
if (num % i == 0) return false;
return true;
}
/**
* Returns the smallest prime number that is strictly larger than
* the specified integer. See {@link #isPrime(int)} for the
* definition of primality.
*
* @param num Base from which to look for the next prime.
* @return Smallest prime number strictly larget than specified
* number.
*/
public static int nextPrime(int num) {
if (num < 2) return 2;
for (int i = num + 1; ; ++i)
if (isPrime(i)) return i;
}
/**
* Converts a natural logarithm to a base 2 logarithm.
* This inverts the operation of {@link #logBase2ToNaturalLog(double)}.
* <p>If the input is <code><i>x</i> = ln <i>z</i></code>, then
* the return value is <code>log<sub>2</sub> <i>z</i></code>.
* Recall that <code>log<sub>2</sub> <i>z</i> = ln <i>z</i> / ln 2.
*
* @param x Natural log of value.
* @return Log base 2 of value.
*/
public static double naturalLogToBase2Log(double x) {
return x * INV_LN_2;
}
/**
* Returns the log base 2 of the specivied value.
*
* @param x Value whose log is taken.
* @return Log of specified value.
*/
public static double log2(double x) {
return naturalLogToBase2Log(java.lang.Math.log(x));
}
/**
* Returns the integer value of reading the specified byte as an
* unsigned value. The computation is carried out by subtracting
* the minimum value, as defined by the constant {@link
* Byte#MIN_VALUE}.
*
* @param b Byte to convert.
* @return Unsigned value of specified byte.
*/
public static int byteAsUnsigned(byte b) {
return (b >= 0) ? (int)b : (256+(int)b);
}
/**
* Returns the log (base 2) of the factorial of the specified long
* integer. The factorial of <code>n</code> is defined for
* <code>n > 0</code> by:
*
* <blockquote><code>
* n!
* = <big><big>Π</big></big><sub><sub>i < 0 <= n</sub></sub> i
* </code></blockquote>
*
* Taking logs of both sides gives:
*
* <blockquote><code>
* log<sub><sub>2</sub></sub> n!
* = <big><big>Σ</big></big><sub><sub>i < 0 <= n</sub></sub>
* log<sub><sub>2</sub></sub> i
* </code></blockquote>
*
* By convention, 0! is taken to be 1, and hence <code>ln 0! = 0</code>.
*
* @param n Specified long integer.
* @return Log of factorial of specified integer.
* @throws IllegalArgumentException If the argument is negative.
*/
public static double log2Factorial(long n) {
if (n < 0) {
String msg = "Factorials only defined for non-negative arguments."
+ " Found argument=" + n;
throw new IllegalArgumentException(msg);
}
double sum = 0.0;
for (long i = 1; i <= n; ++i)
sum += log2(i);
return sum;
}
/**
* Returns the sum of the specified array of double values.
*
* @param xs Variable length list of values, or an array of values.
* @return The sum of the values.
*/
public static double sum(double... xs) {
double sum = 0.0;
for (int i = 0; i < xs.length; ++i)
sum += xs[i];
return sum;
}
/**
* Returns the minimum of the specified array of double values.
* If the length of the array is zero, the result is {@link
* Double#NaN}.
*
* @param xs Variable length list of values, or an array.
* @return Minimum value in array.
*/
public static double minimum(double... xs) {
if (xs.length == 0) return Double.NaN;
double min = xs[0];
for (int i = 1; i < xs.length; ++i)
if (xs[i] < min) min = xs[i];
return min;
}
/**
* Returns the maximum of the specified array of double values.
* If the length of the array is zero, the result is {@link
* Double#NaN}.
*
* @param xs Variable length list of values, or an array.
* @return Maximum value in array.
*/
public static double maximum(double... xs) {
if (xs.length == 0) return Double.NaN;
double max = xs[0];
for (int i = 1; i < xs.length; ++i)
if (xs[i] > max) max = xs[i];
return max;
}
/**
* Returns the log (base 2) of the binomial coefficient of the
* specified arguments. The binomial coefficient is equal to the
* number of ways to choose a subset of size <code>m</code> from a
* set of <code>n</code> objects, which is pronounced "n choose
* m", and is given by:
*
* <blockquote><code>
* choose(n,m) = n! / ( m! * (n-m)!)
* <br>
* log<sub>2</sub> choose(n,m)
* = log<sub>2</sub> n - log<sub>2</sub> m
* - log<sub>2</sub> (n-m)
* </code></blockquote>
*
* @return The log (base 2) of the binomial coefficient of the
* specified arguments.
*/
public static double log2BinomialCoefficient(long n, long m) {
return log2(n) - log2(m) - log2(n-m);
}
static double[] LANCZOS_COEFFS = new double[] {
0.99999999999980993,
676.5203681218851,
-1259.1392167224028,
771.32342877765313,
-176.61502916214059,
12.507343278686905,
-0.13857109526572012,
9.9843695780195716e-6,
1.5056327351493116e-7
};
static double SQRT_2_PI = java.lang.Math.sqrt(2.0 * java.lang.Math.PI);
// assumes input in [0.5,1.5] inclusive
static double lanczosGamma(double z) {
double zMinus1 = z - 1;
double x = LANCZOS_COEFFS[0];
for (int i = 1; i < LANCZOS_COEFFS.length - 2; ++i)
x += LANCZOS_COEFFS[i] / (zMinus1 + i);
double t = zMinus1 + (LANCZOS_COEFFS.length - 2) + 0.5;
return SQRT_2_PI
* java.lang.Math.pow(t, zMinus1 + 0.5)
* java.lang.Math.exp(-t) * x;
}
/**
* Returns the value of the digamma function for the specified
* value. The returned values are accurate to at least 13
* decimal places.
*
* <p>The digamma function is the derivative of the log of the
* gamma function; see the method documentation for {@link
* #log2Gamma(double)} for more information on the gamma function
* itself.
*
* <blockquote><pre>
* Ψ(z)
* = <i>d</i> log Γ(z) / <i>d</i>z
* = Γ'(z) / Γ(z)
* </pre></blockquote>
*
* <p>The numerical approximation is derived from:
*
* <ul>
* <li>Richard J. Mathar. 2005.
* <a href="http://arxiv.org/abs/math/0403344">Chebyshev Series Expansion of Inverse Polynomials</a>.
* <li>
* <li>Richard J. Mathar. 2005.
* <a href="http://www.strw.leidenuniv.nl/~mathar/progs/digamma.c">digamma.c</a>.
* (C Program implementing algorithm.)
* </li>
* </ul>
*
* <i>Implementation Note:</i> The recursive calls in the C
* implementation have been transformed into loops and
* accumulators, and the recursion for values greater than three
* replaced with a simpler reduction. The number of loops
* required before the fixed length expansion is approximately
* integer value of the absolute value of the input. Each loop
* requires a floating point division, two additions and a local
* variable assignment. The fixed portion of the algorithm is
* roughly 30 steps requiring four multiplications, three
* additions, one static final array lookup, and four assignments per
* loop iteration.
*
* @param x Value at which to evaluate the digamma function.
* @return The value of the digamma function at the specified
* value.
*/
public static double digamma(double x)
{
if (x <= 0.0 && (x == (double)((long) x)))
return Double.NaN;
double accum = 0.0;
if (x < 0.0) {
accum += java.lang.Math.PI
/ java.lang.Math.tan(java.lang.Math.PI * (1.0 - x));
x = 1.0 - x;
}
if (x < 1.0 ) {
while (x < 1.0)
accum -= 1.0 / x++;
}
if (x == 1.0)
return accum - NEGATIVE_DIGAMMA_1;
if (x == 2.0)
return accum + 1.0 - NEGATIVE_DIGAMMA_1;
if (x == 3.0)
return accum + 1.5 - NEGATIVE_DIGAMMA_1;
// simpler recursion than Mahar to reduce recursion
if (x > 3.0) {
while (x > 3.0)
accum += 1.0 / --x;
return accum + digamma(x);
}
x -= 2.0;
double tNMinus1 = 1.0;
double tN = x;
double digamma = DIGAMMA_COEFFS[0] + DIGAMMA_COEFFS[1] * tN;
for (int n = 2; n < DIGAMMA_COEFFS.length; n++) {
double tN1 = 2.0 * x * tN - tNMinus1;
digamma += DIGAMMA_COEFFS[n] * tN1;
tNMinus1 = tN;
tN = tN1;
}
return accum + digamma;
}
/**
* The γ constant for computing the digamma function.
*
* <p>The value is defined as the negative of the digamma funtion
* evaluated at 1:
*
* <blockquote><pre>
* γ = - Ψ(1)
*
*/
static double NEGATIVE_DIGAMMA_1 = 0.5772156649015328606065120900824024;
private static final double DIGAMMA_COEFFS[]
= {
.30459198558715155634315638246624251,
.72037977439182833573548891941219706,
-.12454959243861367729528855995001087,
.27769457331927827002810119567456810e-1,
-.67762371439822456447373550186163070e-2,
.17238755142247705209823876688592170e-2,
-.44817699064252933515310345718960928e-3,
.11793660000155572716272710617753373e-3,
-.31253894280980134452125172274246963e-4,
.83173997012173283398932708991137488e-5,
-.22191427643780045431149221890172210e-5,
.59302266729329346291029599913617915e-6,
-.15863051191470655433559920279603632e-6,
.42459203983193603241777510648681429e-7,
-.11369129616951114238848106591780146e-7,
.304502217295931698401459168423403510e-8,
-.81568455080753152802915013641723686e-9,
.21852324749975455125936715817306383e-9,
-.58546491441689515680751900276454407e-10,
.15686348450871204869813586459513648e-10,
-.42029496273143231373796179302482033e-11,
.11261435719264907097227520956710754e-11,
-.30174353636860279765375177200637590e-12,
.80850955256389526647406571868193768e-13,
-.21663779809421233144009565199997351e-13,
.58047634271339391495076374966835526e-14,
-.15553767189204733561108869588173845e-14,
.41676108598040807753707828039353330e-15,
-.11167065064221317094734023242188463e-15 };
/**
* Returns the relative absolute difference between the specified
* values, defined to be:
*
* <blockquote><pre>
* relAbsDiff(x,y) = abs(x-y) / (abs(x) + abs(y))</pre></blockquote>
*
* @param x First value.
* @param y Second value.
* @return The absolute relative difference between the values.
*/
public static double relativeAbsoluteDifference(double x, double y) {
return (Double.isInfinite(x) || Double.isInfinite(y))
? Double.POSITIVE_INFINITY
: (java.lang.Math.abs(x - y)
/ (java.lang.Math.abs(x) + java.lang.Math.abs(y)));
}
/**
* This method returns the log of the sum of the natural
* exponentiated values in the specified array. Mathematically,
* the result is
*
* <blockquote><pre>
* logSumOfExponentials(xs) = log <big><big>( Σ</big></big><sub>i</sub> exp(xs[i]) <big><big>)</big></big></pre></blockquote>
*
* But the result is not calculated directly. Instead, the
* calculation performed is:
*
* <blockquote><pre>
* logSumOfExponentials(xs) = max(xs) + log <big><big>( Σ</big></big><sub>i</sub> exp(xs[i] - max(xs)) <big><big>)</big></big></pre></blockquote>
*
* which produces the same result, but is much more arithmetically
* stable, because the largest value for which <code>exp()</code>
* is calculated is 0.0.
*
* <p>Values of {@code Double.NEGATIVE_INFINITY} are treated as
* having exponentials of 0 and logs of negative infinity.
* That is, they are ignored for the purposes of this computation.
*
* @param xs Array of values.
* @return The log of the sum of the exponentiated values in the
* array.
*/
public static double logSumOfExponentials(double[] xs) {
if (xs.length == 1) return xs[0];
double max = maximum(xs);
double sum = 0.0;
for (int i = 0; i < xs.length; ++i)
if (xs[i] != Double.NEGATIVE_INFINITY)
sum += java.lang.Math.exp(xs[i] - max);
return max + java.lang.Math.log(sum);
}
/**
* Returns the maximum value of an element in xs. If any of the
* values are {@code Double.NaN}, or if the input array is empty,
* the result is {@code Double.NaN}.
*
* @param xs Array in which to find maximum.
* @return Maximum value in array.
*/
public static double max(double... xs) {
if (xs.length == 0)
return Double.NaN;
double max = xs[0];
for (int i = 1; i < xs.length; ++i)
max = java.lang.Math.max(max,xs[i]);
return max;
}
/**
* Returns the maximum value of an element in the specified array.
*
* @param xs Array in which to find maximum.
* @return Maximum value in the array.
* @throws ArrayIndexOutOfBoundsException If the specified array does
* not contai at least one element.
*/
public static int max(int... xs) {
int max = xs[0];
for (int i = 1; i < xs.length; ++i)
if (xs[i] > max)
max = xs[i];
return max;
}
/**
* Returns the sum of the specified integer array. Note that
* there is no check for overflow. If the array is of length 0,
* the sum is defined to be 0.
*
* @param xs Array of integers to sum.
* @return Sum of the array.
*/
public static int sum(int... xs) {
int sum = 0;
for (int i = 0; i < xs.length; ++i)
sum += xs[i];
return sum;
}
}
Related examples in the same category
| 1. | Absolute value | | |
| 2. | Find absolute value of float, int, double and long using Math.abs | | |
| 3. | Find ceiling value of a number using Math.ceil | | |
| 4. | Find exponential value of a number using Math.exp | | |
| 5. | Find floor value of a number using Math.floor | | |
| 6. | Find minimum of two numbers using Math.min | | |
| 7. | Find power using Math.pow | | |
| 8. | Find square root of a number using Math.sqrt | | |
| 9. | Find natural logarithm value of a number using Math.log | | |
| 10. | Find maximum of two numbers using Math.max | | |
| 11. | Get the power value | |  |
| 12. | Using the Math Trig Methods | | 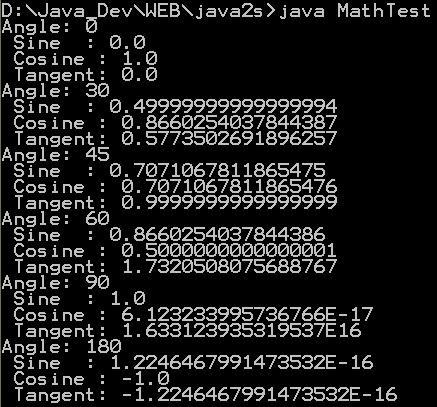 |
| 13. | Using BigDecimal for Precision | | 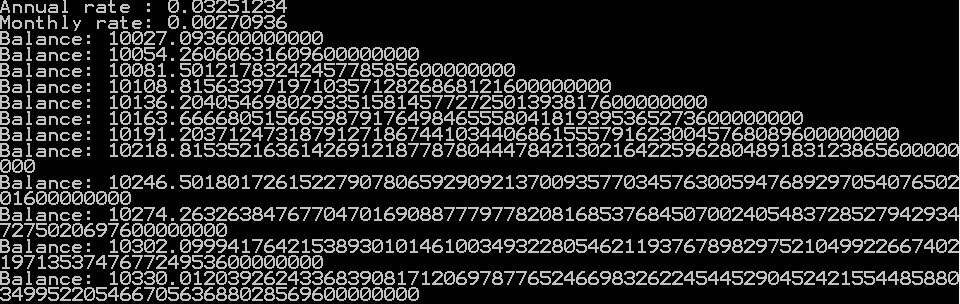 |
| 14. | Demonstrate our own version round() | | 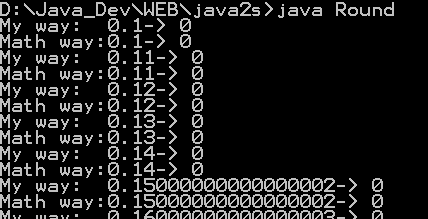 |
| 15. | Demonstrate a few of the Math functions for Trigonometry | |  |
| 16. | Exponential Demo | | 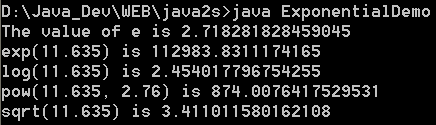 |
| 17. | Min Demo | | |
| 18. | Basic Math Demo | | 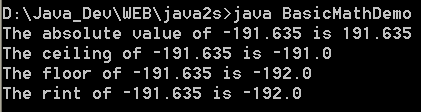 |
| 19. | Using strict math in applications | |  |
| 20. | Conversion between polar and rectangular coordinates | | |
| 21. | Using the pow() function | | |
| 22. | Using strict math at the method level | | |
| 23. | Calculating hyperbolic functions | | |
| 24. | Calculating trigonometric functions | | |
| 25. | Weighted floating-point comparisons | | |
| 26. | Solving right triangles | | |
| 27. | Applying the quadratic formula | | |
| 28. | Calculate the floor of the log, base 2 | | |
| 29. | Greatest Common Divisor (GCD) of positive integer numbers | | |
| 30. | Least Common Multiple (LCM) of two strictly positive integer numbers | | |
| 31. | Moving Average | | |
| 32. | Make Exponention | | |
| 33. | Caclulate the factorial of N | | |
| 34. | Trigonometric Demo | | 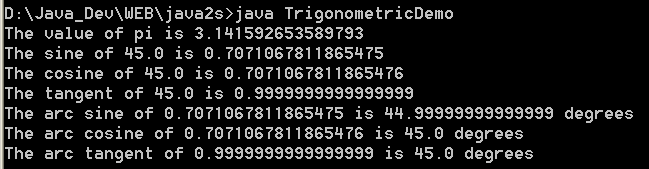 |
| 35. | Complex Number Demo | | |
| 36. | sqrt(a^2 + b^2) without under/overflow | | |
| 37. | Returns an integer hash code representing the given double array value. | | |
| 38. | Returns an integer hash code representing the given double value. | | |
| 39. | Returns n!. Shorthand for n Factorial, the product of the numbers 1,...,n as a double. | | |
| 40. | Returns n!. Shorthand for n Factorial, the product of the numbers 1,...,n. | | |
| 41. | Returns the hyperbolic sine of x. | | |
| 42. | Contains static definition for matrix math methods. | | |
| 43. | For a double precision value x, this method returns +1.0 if x >= 0 and -1.0 if x < 0. Returns NaN if x is NaN. | | |
| 44. | For a float value x, this method returns +1.0F if x >= 0 and -1.0F if x < 0. Returns NaN if x is NaN. | | |
| 45. | Normalize an angle in a 2&pi wide interval around a center value. | | |
| 46. | Normalizes an angle to a relative angle. | | |
| 47. | Normalizes an angle to an absolute angle | | |
| 48. | Normalizes an angle to be near an absolute angle | | |
| 49. | Returns the natural logarithm of n!. | | |
| 50. | Returns the least common multiple between two integer values. | | |
| 51. | Gets the greatest common divisor of the absolute value of two numbers | | |
| 52. | Matrix manipulation | | |
| 53. | Returns exact (http://mathworld.wolfram.com/BinomialCoefficient.html) Binomial Coefficient | | |
| 54. | Returns a double representation of the (http://mathworld.wolfram.com/BinomialCoefficient.html) Binomial Coefficient | | |
| 55. | Returns the natural log of the (http://mathworld.wolfram.com/BinomialCoefficient.html) Binomial Coefficient | | |
| 56. | Returns the hyperbolic cosine of x. | | |
| 57. | Math Utils | | |
| 58. | Implements the methods which are in the standard J2SE's Math class, but are not in in J2ME's. | | |
| 59. | Utility methods for mathematical problems. | | |
| 60. | Computes the binomial coefficient "n over k" | | |
| 61. | Log Gamma | | |
| 62. | Log Beta | | |
| 63. | Beta | | |
| 64. | Gamma | | |
| 65. | Factorial | | |
| 66. | Computes p(x;n,p) where x~B(n,p) | | |
| 67. | Returns the sum of two doubles expressed in log space | | |
| 68. | sigmod | | |
| 69. | sigmod rev | | |
| 70. | Numbers that are closer than this are considered equal | | |
| 71. | Returns the KL divergence, K(p1 || p2). | | |
| 72. | Returns the sum of two doubles expressed in log space | | |
| 73. | Returns the difference of two doubles expressed in log space | | |
| 74. | Is Prime | | |
| 75. | Statistical functions on arrays of numbers, namely, the mean, variance, standard deviation, covariance, min and max | | |
| 76. | This class calculates the Factorial of a numbers passed into the program through command line arguments. | |  |
| 77. | Calculates the Greatest Common Divisor of two numbers passed into the program through command line arguments. | | |
| 78. | Variance: the square of the standard deviation. | | |
| 79. | Population Standard Deviation | | |
| 80. | Returns from a static prime table the least prime that is greater than or equal to a specified value. | | |