Calculate the floor of the log, base 2 : Math « Development Class « Java

1. Java
2. Development Class
3. Math

Calculate the floor of the log, base 2

        
/*
 * $RCSfile: MathUtil.java,v $
 * $Revision: 1.1 $
 * $Date: 2005/02/11 05:02:25 $
 * $State: Exp $
 *
 * Class:                   MathUtil
 *
 * Description:             Utility mathematical methods
 *
 *
 *
 * COPYRIGHT:
 *
 * This software module was originally developed by Raphal Grosbois and
 * Diego Santa Cruz (Swiss Federal Institute of Technology-EPFL); Joel
 * Askelf (Ericsson Radio Systems AB); and Bertrand Berthelot, David
 * Bouchard, Flix Henry, Gerard Mozelle and Patrice Onno (Canon Research
 * Centre France S.A) in the course of development of the JPEG2000
 * standard as specified by ISO/IEC 15444 (JPEG 2000 Standard). This
 * software module is an implementation of a part of the JPEG 2000
 * Standard. Swiss Federal Institute of Technology-EPFL, Ericsson Radio
 * Systems AB and Canon Research Centre France S.A (collectively JJ2000
 * Partners) agree not to assert against ISO/IEC and users of the JPEG
 * 2000 Standard (Users) any of their rights under the copyright, not
 * including other intellectual property rights, for this software module
 * with respect to the usage by ISO/IEC and Users of this software module
 * or modifications thereof for use in hardware or software products
 * claiming conformance to the JPEG 2000 Standard. Those intending to use
 * this software module in hardware or software products are advised that
 * their use may infringe existing patents. The original developers of
 * this software module, JJ2000 Partners and ISO/IEC assume no liability
 * for use of this software module or modifications thereof. No license
 * or right to this software module is granted for non JPEG 2000 Standard
 * conforming products. JJ2000 Partners have full right to use this
 * software module for his/her own purpose, assign or donate this
 * software module to any third party and to inhibit third parties from
 * using this software module for non JPEG 2000 Standard conforming
 * products. This copyright notice must be included in all copies or
 * derivative works of this software module.
 *
 * Copyright (c) 1999/2000 JJ2000 Partners.
 * */



/**
 * This class contains a collection of utility methods fro mathematical
 * operations. All methods are static.
 * */
public class MathUtil {

    /**
     * Method that calculates the floor of the log, base 2,
     * of 'x'. The calculation is performed in integer arithmetic,
     * therefore, it is exact.
     *
     * @param x The value to calculate log2 on.
     *
     * @return floor(log(x)/log(2)), calculated in an exact way.
     * */
    public static int log2(int x) {
        int y,v;
        // No log of 0 or negative
        if (x <= 0) {
            throw new IllegalArgumentException(""+x+" <= 0");
        }
        // Calculate log2 (it's actually floor log2)
        v = x;
        y = -1;
        while (v>0) {
            v >>=1;
            y++;
        }
        return y;
    }

   
}

   
    
    
    
    
    
    
    
  

Related examples in the same category

1.	Absolute value
2.	Find absolute value of float, int, double and long using Math.abs
3.	Find ceiling value of a number using Math.ceil
4.	Find exponential value of a number using Math.exp
5.	Find floor value of a number using Math.floor
6.	Find minimum of two numbers using Math.min
7.	Find power using Math.pow
8.	Find square root of a number using Math.sqrt
9.	Find natural logarithm value of a number using Math.log
10.	Find maximum of two numbers using Math.max
11.	Get the power value
12.	Using the Math Trig Methods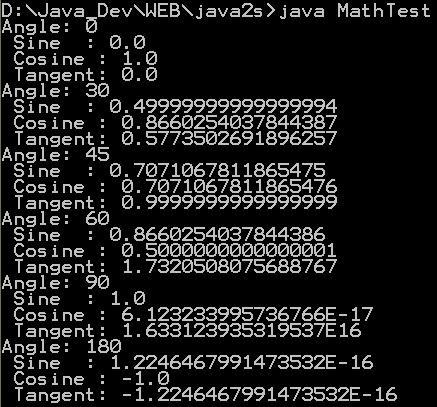
13.	Using BigDecimal for Precision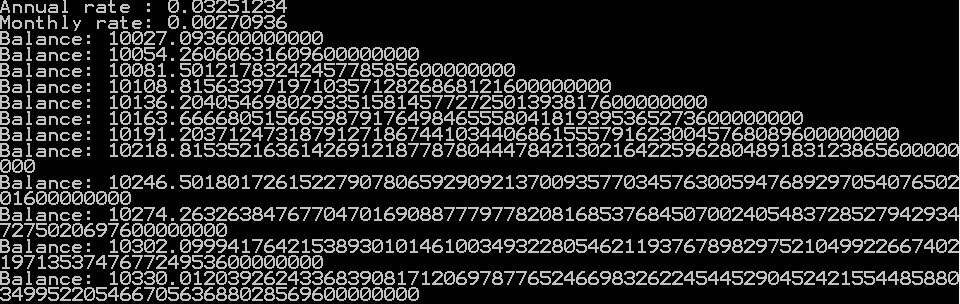
14.	Demonstrate our own version round()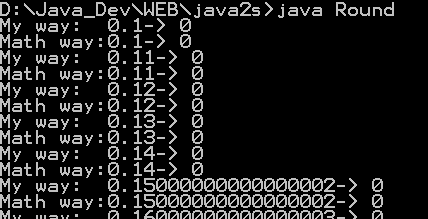
15.	Demonstrate a few of the Math functions for Trigonometry
16.	Exponential Demo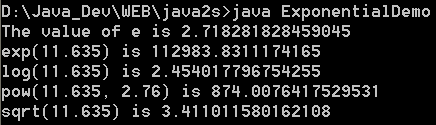
17.	Min Demo
18.	Basic Math Demo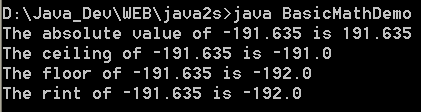
19.	Using strict math in applications
20.	Conversion between polar and rectangular coordinates
21.	Using the pow() function
22.	Using strict math at the method level
23.	Calculating hyperbolic functions
24.	Calculating trigonometric functions
25.	Weighted floating-point comparisons
26.	Solving right triangles
27.	Applying the quadratic formula
28.	Greatest Common Divisor (GCD) of positive integer numbers
29.	Least Common Multiple (LCM) of two strictly positive integer numbers
30.	Moving Average
31.	Make Exponention
32.	Caclulate the factorial of N
33.	Trigonometric Demo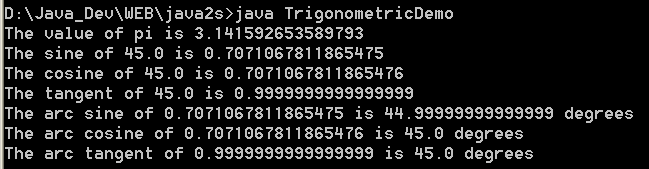
34.	Complex Number Demo
35.	sqrt(a^2 + b^2) without under/overflow
36.	Returns an integer hash code representing the given double array value.
37.	Returns an integer hash code representing the given double value.
38.	Returns n!. Shorthand for n Factorial, the product of the numbers 1,...,n as a double.
39.	Returns n!. Shorthand for n Factorial, the product of the numbers 1,...,n.
40.	Returns the hyperbolic sine of x.
41.	Contains static definition for matrix math methods.
42.	For a double precision value x, this method returns +1.0 if x >= 0 and -1.0 if x < 0. Returns NaN if x is NaN.
43.	For a float value x, this method returns +1.0F if x >= 0 and -1.0F if x < 0. Returns NaN if x is NaN.
44.	Normalize an angle in a 2&pi wide interval around a center value.
45.	Normalizes an angle to a relative angle.
46.	Normalizes an angle to an absolute angle
47.	Normalizes an angle to be near an absolute angle
48.	Returns the natural logarithm of n!.
49.	Returns the least common multiple between two integer values.
50.	Gets the greatest common divisor of the absolute value of two numbers
51.	Matrix manipulation
52.	Returns exact (http://mathworld.wolfram.com/BinomialCoefficient.html) Binomial Coefficient
53.	Returns a double representation of the (http://mathworld.wolfram.com/BinomialCoefficient.html) Binomial Coefficient
54.	Returns the natural log of the (http://mathworld.wolfram.com/BinomialCoefficient.html) Binomial Coefficient
55.	Returns the hyperbolic cosine of x.
56.	Math Utils
57.	Implements the methods which are in the standard J2SE's Math class, but are not in in J2ME's.
58.	Utility methods for mathematical problems.
59.	A math utility class with static methods.
60.	Computes the binomial coefficient "n over k"
61.	Log Gamma
62.	Log Beta
63.	Beta
64.	Gamma
65.	Factorial
66.	Computes p(x;n,p) where x~B(n,p)
67.	Returns the sum of two doubles expressed in log space
68.	sigmod
69.	sigmod rev
70.	Numbers that are closer than this are considered equal
71.	Returns the KL divergence, K(p1 || p2).
72.	Returns the sum of two doubles expressed in log space
73.	Returns the difference of two doubles expressed in log space
74.	Is Prime
75.	Statistical functions on arrays of numbers, namely, the mean, variance, standard deviation, covariance, min and max
76.	This class calculates the Factorial of a numbers passed into the program through command line arguments.
77.	Calculates the Greatest Common Divisor of two numbers passed into the program through command line arguments.
78.	Variance: the square of the standard deviation.
79.	Population Standard Deviation
80.	Returns from a static prime table the least prime that is greater than or equal to a specified value.