Contains static definition for matrix math methods.
/*
* Soya3D
* Copyright (C) 1999-2000 Jean-Baptiste LAMY (Artiste on the web)
*
* This program is free software; you can redistribute it and/or modify
* it under the terms of the GNU Library General Public License as published by
* the Free Software Foundation; either version 2 of the License, or
* (at your option) any later version.
*
* This program is distributed in the hope that it will be useful,
* but WITHOUT ANY WARRANTY; without even the implied warranty of
* MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
* GNU General Public License for more details.
*
* You should have received a copy of the GNU Library General Public License
* along with this program; if not, write to the Free Software
* Foundation, Inc., 59 Temple Place, Suite 330, Boston, MA 02111-1307 USA
*/
/**
* Contains static definition for matrix math methods.
*
* Here, a matrix is a float[16], and a vector or a point a float[3] (contrary to other part of Opale.Soya, where a point is 3 coords + a CoordSyst).
*
* @author Artiste on the Web
*/
public class Matrix extends Object {
private Matrix() { }
/**
* The value of PI in float.
*/
public static final float PI = (float) java.lang.Math.PI;
public static final float EPSILON = 0.001f;
public static float pow2(float f) { return f*f; }
private static float[][] stock = new float[1000][];
/**
* Inverts a 4*4 matrix. Warning : this method works only if m[3] = m[7] = m[11] = 0f
* and m[15] = 1f.
* @param m the matrix
* @return the inverted matrix or null if m is not invertable
*/
public static final float[] matrixInvert(float[] m) { // Optimized!
float[] r = matrixInvert3_3(m);
if(r == null) return null;
r[12] = -(m[12] * r[0] + m[13] * r[4] + m[14] * r[ 8]);
r[13] = -(m[12] * r[1] + m[13] * r[5] + m[14] * r[ 9]);
r[14] = -(m[12] * r[2] + m[13] * r[6] + m[14] * r[10]);
return r;
}
/**
* Inverts a 3*3 part of a 4*4 matrix.
* It IS NOT a complete inversion because other values in the matrix (such as the translation part) are set to 0.
* It isn't a bug, other classes assume this.
* @param m the matrix that will be inverted
* @return the inverted matrix. Value 12, 13, 14 that represent the translation are set to 0. Return null if the matrix is not invertable
*/
public static final float[] matrixInvert3_3(float[] m) {
float[] r = new float[16];
float det = m[0] * (m[5] * m[10] - m[9] * m[6])
- m[4] * (m[1] * m[10] - m[9] * m[2])
+ m[8] * (m[1] * m[ 6] - m[5] * m[2]);
if(det == 0f) return null;
det = 1f / det;
r[ 0] = det * (m[5] * m[10] - m[9] * m[6]);
r[ 4] = - det * (m[4] * m[10] - m[8] * m[6]);
r[ 8] = det * (m[4] * m[ 9] - m[8] * m[5]);
r[ 1] = - det * (m[1] * m[10] - m[9] * m[2]);
r[ 5] = det * (m[0] * m[10] - m[8] * m[2]);
r[ 9] = - det * (m[0] * m[ 9] - m[8] * m[1]);
r[ 2] = det * (m[1] * m[ 6] - m[5] * m[2]);
r[ 6] = - det * (m[0] * m[ 6] - m[4] * m[2]);
r[10] = det * (m[0] * m[ 5] - m[4] * m[1]);
r[15] = 1f;
return r;
}
/**
* Multiply a 4*4 matrix by another, as if they were 3*3.
* @param a the first / left matrix
* @param b the second / right matrix
* @return the result
*/
public static final float[] matrixMultiply(float[] b, float[] a) {
float[] r = new float[16];
r[ 0] = a[ 0] * b[ 0] + a[ 1] * b[ 4] + a[ 2] * b[ 8];
r[ 4] = a[ 4] * b[ 0] + a[ 5] * b[ 4] + a[ 6] * b[ 8];
r[ 8] = a[ 8] * b[ 0] + a[ 9] * b[ 4] + a[10] * b[ 8];
r[12] = a[12] * b[ 0] + a[13] * b[ 4] + a[14] * b[ 8] + b[12];
r[ 1] = a[ 0] * b[ 1] + a[ 1] * b[ 5] + a[ 2] * b[ 9];
r[ 5] = a[ 4] * b[ 1] + a[ 5] * b[ 5] + a[ 6] * b[ 9];
r[ 9] = a[ 8] * b[ 1] + a[ 9] * b[ 5] + a[10] * b[ 9];
r[13] = a[12] * b[ 1] + a[13] * b[ 5] + a[14] * b[ 9] + b[13];
r[ 2] = a[ 0] * b[ 2] + a[ 1] * b[ 6] + a[ 2] * b[10];
r[ 6] = a[ 4] * b[ 2] + a[ 5] * b[ 6] + a[ 6] * b[10];
r[10] = a[ 8] * b[ 2] + a[ 9] * b[ 6] + a[10] * b[10];
r[14] = a[12] * b[ 2] + a[13] * b[ 6] + a[14] * b[10] + b[14];
r[ 3] = 0;
r[ 7] = 0;
r[11] = 0;
r[15] = 1;
return r;
}
/**
* Multiply a 4*4 matrix by another.
* @param a the first / left matrix
* @param b the second / right matrix
* @return the result
*/
public static final float[] matrixMultiply_4(float[] b, float[] a) {
float[] r = new float[16];
r[ 0] = a[ 0] * b[ 0] + a[ 1] * b[ 4] + a[ 2] * b[ 8] + a[ 3] * b[12];
r[ 4] = a[ 4] * b[ 0] + a[ 5] * b[ 4] + a[ 6] * b[ 8] + a[ 7] * b[12];
r[ 8] = a[ 8] * b[ 0] + a[ 9] * b[ 4] + a[10] * b[ 8] + a[11] * b[12];
r[12] = a[12] * b[ 0] + a[13] * b[ 4] + a[14] * b[ 8] + a[15] * b[12];
r[ 1] = a[ 0] * b[ 1] + a[ 1] * b[ 5] + a[ 2] * b[ 9] + a[ 3] * b[13];
r[ 5] = a[ 4] * b[ 1] + a[ 5] * b[ 5] + a[ 6] * b[ 9] + a[ 7] * b[13];
r[ 9] = a[ 8] * b[ 1] + a[ 9] * b[ 5] + a[10] * b[ 9] + a[11] * b[13];
r[13] = a[12] * b[ 1] + a[13] * b[ 5] + a[14] * b[ 9] + a[15] * b[13];
r[ 2] = a[ 0] * b[ 2] + a[ 1] * b[ 6] + a[ 2] * b[10] + a[ 3] * b[14];
r[ 6] = a[ 4] * b[ 2] + a[ 5] * b[ 6] + a[ 6] * b[10] + a[ 7] * b[14];
r[10] = a[ 8] * b[ 2] + a[ 9] * b[ 6] + a[10] * b[10] + a[11] * b[14];
r[14] = a[12] * b[ 2] + a[13] * b[ 6] + a[14] * b[10] + a[15] * b[14];
r[ 3] = a[ 0] * b[ 3] + a[ 1] * b[ 7] + a[ 2] * b[11] + a[ 3] * b[15];
r[ 7] = a[ 4] * b[ 3] + a[ 5] * b[ 7] + a[ 6] * b[11] + a[ 7] * b[15];
r[11] = a[ 8] * b[ 3] + a[ 9] * b[ 7] + a[10] * b[11] + a[11] * b[15];
r[15] = a[12] * b[ 3] + a[13] * b[ 7] + a[14] * b[11] + a[15] * b[15];
return r;
}
/**
* Multiply a point by a 4*4 matrix.
* @param m the matrix
* @param p the point
* the resulting point
*/
public static final float[] pointMultiplyByMatrix(float[] m, float[] p) { // Assume v[3] = 1.
float[] r = { p[0] * m[0] + p[1] * m[4] + p[2] * m[ 8] + m[12],
p[0] * m[1] + p[1] * m[5] + p[2] * m[ 9] + m[13],
p[0] * m[2] + p[1] * m[6] + p[2] * m[10] + m[14]
};
return r;
}
/**
* Multiply a vector by a 4*4 matrix.
* @param m the matrix
* @param v the vector
* @return the resulting vector
*/
public static final float[] vectorMultiplyByMatrix(float[] m, float[] v) {
float[] r = { v[0] * m[0] + v[1] * m[4] + v[2] * m[ 8],
v[0] * m[1] + v[1] * m[5] + v[2] * m[ 9],
v[0] * m[2] + v[1] * m[6] + v[2] * m[10]
};
return r;
}
/**
* Compare 2 matrix.
* @param a the first matrix
* @param b the second matrix
* @return true if a and b are equal (or very near)
*/
public static final boolean matrixEqual(float[] a, float[] b) {
for(int i = 0; i < 16; i++) {
if(Math.abs(a[i] - b[i]) > EPSILON) return false;
}
return true;
}
/**
* Convert a matrix into a string. Useful for debuging soya.
* @param m the matrix
* @return the string
*/
public static final String matrixToString(float[] m) {
String s = "matrix 4_4 {\n";
s = s + Float.toString(m[ 0]) + " " + Float.toString(m[ 4]) + " " + Float.toString(m[ 8]) + "\n";
s = s + Float.toString(m[ 1]) + " " + Float.toString(m[ 5]) + " " + Float.toString(m[ 9]) + "\n";
s = s + Float.toString(m[ 2]) + " " + Float.toString(m[ 6]) + " " + Float.toString(m[10]) + "\n";
s = s + Float.toString(m[ 3]) + " " + Float.toString(m[ 7]) + " " + Float.toString(m[11]) + "\n";
s = s + "X: " + Float.toString(m[12]) + " Y: " + Float.toString(m[13]) + " Z: " + Float.toString(m[14]) + " W: " + Float.toString(m[15]) + "\n";
s = s + "}";
return s;
}
/**
* Create a new identity matrix.
* @return an identity matrix
*/
public static final float[] matrixIdentity() {
float[] m = new float[16];
matrixIdentity(m);
return m;
}
/**
* Set a matrix to identity matrix.
* @param m the matrix
*/
public static final void matrixIdentity(float[] m) {
m[ 0] = 1f;
m[ 1] = 0f;
m[ 2] = 0f;
m[ 3] = 0f;
m[ 4] = 0f;
m[ 5] = 1f;
m[ 6] = 0f;
m[ 7] = 0f;
m[ 8] = 0f;
m[ 9] = 0f;
m[10] = 1f;
m[11] = 0f;
m[12] = 0f;
m[13] = 0f;
m[14] = 0f;
m[15] = 1f;
}
/**
* Create a scale matrix.
* @param x the x factor of the scaling
* @param y the y factor of the scaling
* @param z the z factor of the scaling
* @return the matrix
*/
public static float[] matrixScale(float x, float y, float z) {
float[] m2 = { x, 0f, 0f, 0f,
0f, y, 0f, 0f,
0f, 0f, z, 0f,
0f, 0f, 0f, 1f };
return m2;
}
/**
* Scale a matrix (this is equivalent to OpenGL glScale* ).
* @param m the matrix
* @param x the x factor of the scaling
* @param y the y factor of the scaling
* @param z the z factor of the scaling
* @return the scaled matrix
*/
public static float[] matrixScale(float[] m, float x, float y, float z) {
float r[] = new float[16];
r[ 0] = x * m[ 0];
r[ 4] = y * m[ 4];
r[ 8] = z * m[ 8];
r[12] = m[12];
r[ 1] = x * m[ 1];
r[ 5] = y * m[ 5];
r[ 9] = z * m[ 9];
r[13] = m[13];
r[ 2] = x * m[ 2];
r[ 6] = y * m[ 6];
r[10] = z * m[10];
r[14] = m[14];
r[ 3] = 0;
r[ 7] = 0;
r[11] = 0;
r[15] = 1;
return r;
// return matrixMultiply(m, matrixScale(x, y, z));
}
/**
* Create a lateral rotation matrix (lateral rotation is around a (0, 1, 0) axis).
* @param angle the angle of the rotation
* @return the matrix
*/
public static float[] matrixRotateLateral(float angle) {
if(angle == 0f) return matrixIdentity();
angle = (float) Math.toRadians(angle);
float cos = (float) java.lang.Math.cos(angle);
float sin = (float) java.lang.Math.sin(angle);
float[] m2 = { cos, 0f, -sin, 0f,
0f , 1f, 0f , 0f,
sin, 0f, cos, 0f,
0f , 0f, 0f , 1f };
return m2;
}
/**
* Laterally rotate a matrix (lateral rotation is around a (0, 1, 0) axis).
* @param angle the angle of the rotation
* @param m the matrix to rotate
* @return the resulting matrix
*/
public static float[] matrixRotateLateral(float[] m, float angle) {
if(angle == 0f) return matrixIdentity();
angle = (float) Math.toRadians(angle);
float cos = (float) java.lang.Math.cos(angle);
float sin = (float) java.lang.Math.sin(angle);
float r[] = new float[16];
r[ 0] = m[ 0] * cos + m[ 2] * sin;
r[ 4] = m[ 4] * cos + m[ 6] * sin;
r[ 8] = m[ 8] * cos + m[10] * sin;
r[12] = m[12] * cos + m[14] * sin;
r[ 1] = m[ 1];
r[ 5] = m[ 5];
r[ 9] = m[ 9];
r[13] = m[13];
r[ 2] = -m[ 0] * sin + m[ 2] * cos;
r[ 6] = -m[ 4] * sin + m[ 6] * cos;
r[10] = -m[ 8] * sin + m[10] * cos;
r[14] = -m[12] * sin + m[14] * cos;
r[ 3] = 0;
r[ 7] = 0;
r[11] = 0;
r[15] = 1;
return r;
// return matrixMultiply(matrixRotateLateral(angle), m);
}
/**
* Create a vertical rotation matrix (vertical rotation is around a (1, 0, 0) axis).
* @param angle the angle of the rotation
* @return the matrix
*/
public static float[] matrixRotateVertical(float angle) {
if(angle == 0f) return matrixIdentity();
angle = (float) Math.toRadians(angle);
float cos = (float) java.lang.Math.cos(angle);
float sin = (float) java.lang.Math.sin(angle);
float[] m2 = { 1f, 0f , 0f , 0f,
0f, cos, sin, 0f,
0f, -sin, cos, 0f,
0f, 0f , 0f , 1f };
return m2;
}
/**
* Vertically rotate a matrix (vertical rotation is around a (1, 0, 0) axis).
* @param angle the angle of the rotation
* @param m the matrix to rotate
* @return the resulting matrix
*/
public static float[] matrixRotateVertical(float[] m, float angle) {
if(angle == 0f) return matrixIdentity();
angle = (float) Math.toRadians(angle);
float cos = (float) java.lang.Math.cos(angle);
float sin = (float) java.lang.Math.sin(angle);
float r[] = new float[16];
r[ 0] = m[ 0];
r[ 4] = m[ 4];
r[ 8] = m[ 8];
r[12] = m[12];
r[ 1] = m[ 1] * cos - m[ 2] * sin;
r[ 5] = m[ 5] * cos - m[ 6] * sin;
r[ 9] = m[ 9] * cos - m[10] * sin;
r[13] = m[13] * cos - m[14] * sin;
r[ 2] = m[ 1] * sin + m[ 2] * cos;
r[ 6] = m[ 5] * sin + m[ 6] * cos;
r[10] = m[ 9] * sin + m[10] * cos;
r[14] = m[13] * sin + m[14] * cos;
r[ 3] = 0;
r[ 7] = 0;
r[11] = 0;
r[15] = 1;
return r;
// return matrixMultiply(matrixRotateVertical(angle), m);
}
/**
* Create a incline-rotation matrix (incline-rotation is around a (0, 0, 1) axis).
* @param angle the angle of the rotation
* @return the matrix
*/
public static float[] matrixRotateIncline(float angle) {
if(angle == 0f) return matrixIdentity();
angle = (float) Math.toRadians(angle);
float cos = (float) java.lang.Math.cos(angle);
float sin = (float) java.lang.Math.sin(angle);
float m2[] = { cos, sin, 0f, 0f,
-sin, cos, 0f, 0f,
0f , 0f , 1f, 0f,
0f , 0f , 0f, 1f };
return m2;
}
/**
* Incline a matrix (incline-rotation is around a (0, 0, 1) axis).
* @param angle the angle of the rotation
* @param m the matrix to rotate
* @return the resulting matrix
*/
public static float[] matrixRotateIncline(float[] m, float angle) {
if(angle == 0f) return matrixIdentity();
angle = (float) Math.toRadians(angle);
float cos = (float) java.lang.Math.cos(angle);
float sin = (float) java.lang.Math.sin(angle);
float r[] = new float[16];
r[ 0] = m[ 0] * cos - m[ 1] * sin;
r[ 4] = m[ 4] * cos - m[ 5] * sin;
r[ 8] = m[ 8] * cos - m[ 9] * sin;
r[12] = m[12] * cos - m[13] * sin;
r[ 1] = m[ 0] * sin + m[ 1] * cos;
r[ 5] = m[ 4] * sin + m[ 5] * cos;
r[ 9] = m[ 8] * sin + m[ 9] * cos;
r[13] = m[12] * sin + m[13] * cos;
r[ 2] = m[ 2];
r[ 6] = m[ 6];
r[10] = m[10];
r[14] = m[14];
r[ 3] = 0;
r[ 7] = 0;
r[11] = 0;
r[15] = 1;
return r;
// return matrixMultiply(matrixRotateIncline(angle), m);
}
/**
* Create a rotation matrix.
* @param angle the angle of the rotation
* @param x the x coordinate of the rotation axis
* @param y the y coordinate of the rotation axis
* @param z the z coordinate of the rotation axis
* @return the matrix
*/
public static float[] matrixRotate(float angle, float x, float y, float z) {
if(angle == 0f) return matrixIdentity();
angle = (float) Math.toRadians(angle);
float d = (float) java.lang.Math.sqrt(java.lang.Math.pow(x, 2) + java.lang.Math.pow(y, 2) + java.lang.Math.pow(z, 2));
if(d != 1f) {
x = x / d;
y = y / d;
z = z / d;
}
float cos = (float) java.lang.Math.cos(angle);
float sin = (float) java.lang.Math.sin(angle);
float co1 = 1f - cos;
float m2[] = { x * x * co1 + cos , y * x * co1 + z * sin, z * x * co1 - y * sin, 0f,
x * y * co1 - z * sin, y * y * co1 + cos , z * y * co1 + x * sin, 0f,
x * z * co1 + y * sin, y * z * co1 - x * sin, z * z * co1 + cos , 0f,
0f , 0f , 0f , 1f };
return m2;
}
/**
* Rotate a matrix (this is equivalent to OpenGL glRotate*).
* @param m the matrix to rotate
* @param angle the angle of the rotation
* @param x the x coordinate of the rotation axis
* @param y the y coordinate of the rotation axis
* @param z the z coordinate of the rotation axis
* @return the resulting matrix
*/
public static float[] matrixRotate(float[] m, float angle, float x, float y, float z) {
return matrixMultiply(matrixRotate(angle, x, y, z), m);
}
/**
* Rotation about an arbitrary Axis
* @param alpha the angle of the rotation
* @param p1 first axis point
* @param p2 second axis point
* @return the rotation matrix
*/
public static float[] matrixRotate(float alpha, float[] p1, float[] p2){
alpha = alpha * PI / 180f;
float a1 = p1[0];
float a2 = p1[1];
float a3 = p1[2];
//Compute the vector defines by point p1 and p2
float v1 = p2[0] - a1 ;
float v2 = p2[1] - a2 ;
float v3 = p2[2] - a3 ;
double theta = Math.atan2(v2, v1);
double phi = Math.atan2(Math.sqrt(v1 * v1 + v2 * v2), v3);
float cosAlpha, sinAlpha, sinPhi2;
float cosTheta, sinTheta, cosPhi2;
float cosPhi, sinPhi, cosTheta2, sinTheta2 ;
cosPhi = (float) Math.cos(phi); cosTheta = (float) Math.cos(theta) ; cosTheta2 = (float) cosTheta * cosTheta ;
sinPhi = (float) Math.sin(phi); sinTheta = (float) Math.sin(theta) ; sinTheta2 = (float) sinTheta * sinTheta ;
sinPhi2 = (float) sinPhi*sinPhi ;
cosPhi2 = (float) cosPhi*cosPhi ;
cosAlpha = (float) Math.cos(alpha) ;
sinAlpha = (float) Math.sin(alpha) ;
float c = (float) 1.0 - cosAlpha ;
float r11,r12,r13,r14,r21,r22,r23,r24,r31,r32,r33,r34;
r11 = cosTheta2 * ( cosAlpha * cosPhi2 +sinPhi2 ) + cosAlpha * sinTheta2 ;
r12 = sinAlpha * cosPhi + c * sinPhi2 * cosTheta * sinTheta ;
r13 = sinPhi * (cosPhi * cosTheta * c - sinAlpha*sinTheta) ;
r21 = sinPhi2 * cosTheta * sinTheta*c - sinAlpha*cosPhi ;
r22 = sinTheta2 * (cosAlpha*cosPhi2 +sinPhi2) + cosAlpha*cosTheta2 ;
r23 = sinPhi * (cosPhi*sinTheta*c + sinAlpha*cosTheta);
r31 = sinPhi * (cosPhi*cosTheta*c + sinAlpha*sinTheta);
r32 = sinPhi * (cosPhi*sinTheta*c - sinAlpha*cosTheta);
r33 = cosAlpha * sinPhi2 + cosPhi2 ;
r14 = a1 - a1*r11 - a2*r21 - a3*r31 ;
r24 = a2 - a1*r12 - a2*r22 - a3*r32 ;
r34 = a3 - a1*r13 - a2*r23 - a3*r33 ;
float[] m2 = { r11 , r12 , r13 , 0f,
r21 , r22 , r23 , 0f,
r31 , r32 , r33 , 0f,
r14 , r24 , r34 , 1f
};
return m2;
}
/**
* Rotation about an arbitrary Axis
* @param m the matrix to rotate
* @param alpha the angle of the rotation
* @param p1 first axis point
* @param p2 second axis point
* @return the rotated matrix
*/
public static float[] matrixRotate(float[] m, float alpha, float[] p1, float[] p2) {
return matrixMultiply(matrixRotate(alpha, p1, p2), m);
}
/**
* Create a translation matrix.
* @param x the x coordinate of the translation vector
* @param y the y coordinate of the translation vector
* @param z the z coordinate of the translation vector
* @return the translation matrix
*/
public static float[] matrixTranslate(float x, float y, float z) {
float m2[] = { 1f, 0f, 0f, 0f,
0f, 1f, 0f, 0f,
0f, 0f, 1f, 0f,
x , y , z , 1f };
return m2;
}
/**
* Translate a matrix (this is equivalent to OpenGL glTranslate*).
* @param m the matrix to translate
* @param x the x coordinate of the translation vector
* @param y the y coordinate of the translation vector
* @param z the z coordinate of the translation vector
* @return the resulting matrix
*/
public static float[] matrixTranslate(float[] m, float x, float y, float z) {
float[] r = new float[16];
System.arraycopy(m, 0, r, 0, 12);
r[12] = m[12] + x;
r[13] = m[13] + y;
r[14] = m[14] + z;
r[15] = 1f;
return r;
//return matrixMultiply(matrixTranslate(x, y, z), m);
}
public static float[] matrixPerspective(float fovy, float aspect, float znear, float zfar) {
// this code is adapted from Mesa :)
float xmax, ymax;
ymax = znear * (float) Math.tan(Math.toRadians(fovy / 2f));
xmax = aspect * ymax;
return matrixFrustum(-xmax, xmax, -ymax, ymax, znear, zfar);
}
public static float[] matrixFrustum(float left, float right, float bottom, float top, float near, float far) {
// this code is adapted from Mesa :)
float x, y, a, b, c, d;
float[] r = new float[16];
r[14] = right - left;
r[10] = top - bottom;
r[0 ] = 2f * near;
r[5 ] = r[0] / r[10];
r[0 ] = r[0] / r[14];
r[8 ] = (right + left) / r[14];
r[9 ] = (top + bottom) / r[10];
r[14] = far - near;
r[10] = -(far + near) / r[14];
r[14] = -(2f * far * near) / r[14]; // error ? (this rem was in Mesa)
r[1 ] = 0f;
r[2 ] = 0f;
r[3 ] = 0f;
r[4 ] = 0f;
r[6 ] = 0f;
r[7 ] = 0f;
r[11] = -1f;
r[12] = 0f;
r[13] = 0f;
r[15] = 0f;
return r;
}
}
Related examples in the same category
| 1. | Absolute value | | |
| 2. | Find absolute value of float, int, double and long using Math.abs | | |
| 3. | Find ceiling value of a number using Math.ceil | | |
| 4. | Find exponential value of a number using Math.exp | | |
| 5. | Find floor value of a number using Math.floor | | |
| 6. | Find minimum of two numbers using Math.min | | |
| 7. | Find power using Math.pow | | |
| 8. | Find square root of a number using Math.sqrt | | |
| 9. | Find natural logarithm value of a number using Math.log | | |
| 10. | Find maximum of two numbers using Math.max | | |
| 11. | Get the power value | |  |
| 12. | Using the Math Trig Methods | | 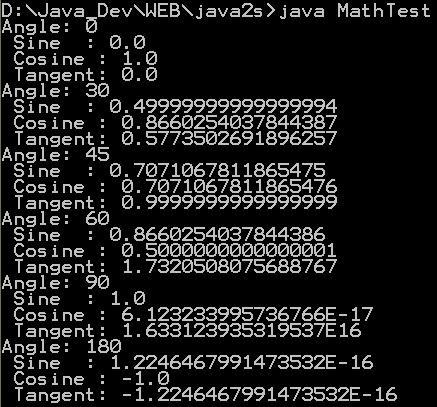 |
| 13. | Using BigDecimal for Precision | | 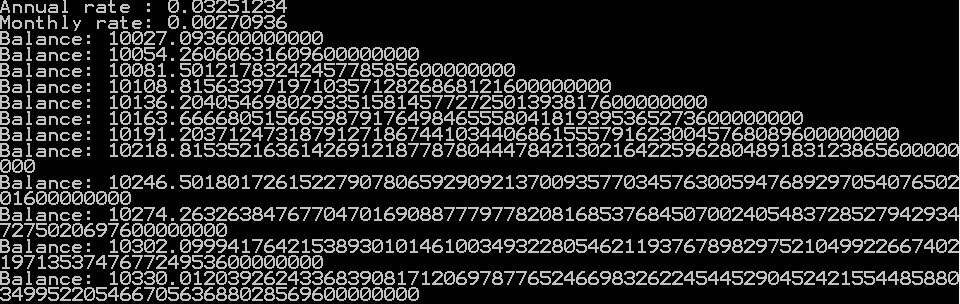 |
| 14. | Demonstrate our own version round() | | 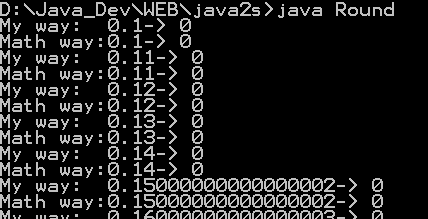 |
| 15. | Demonstrate a few of the Math functions for Trigonometry | |  |
| 16. | Exponential Demo | | 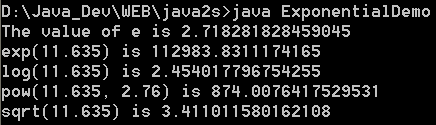 |
| 17. | Min Demo | | |
| 18. | Basic Math Demo | | 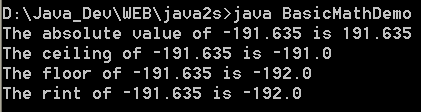 |
| 19. | Using strict math in applications | |  |
| 20. | Conversion between polar and rectangular coordinates | | |
| 21. | Using the pow() function | | |
| 22. | Using strict math at the method level | | |
| 23. | Calculating hyperbolic functions | | |
| 24. | Calculating trigonometric functions | | |
| 25. | Weighted floating-point comparisons | | |
| 26. | Solving right triangles | | |
| 27. | Applying the quadratic formula | | |
| 28. | Calculate the floor of the log, base 2 | | |
| 29. | Greatest Common Divisor (GCD) of positive integer numbers | | |
| 30. | Least Common Multiple (LCM) of two strictly positive integer numbers | | |
| 31. | Moving Average | | |
| 32. | Make Exponention | | |
| 33. | Caclulate the factorial of N | | |
| 34. | Trigonometric Demo | | 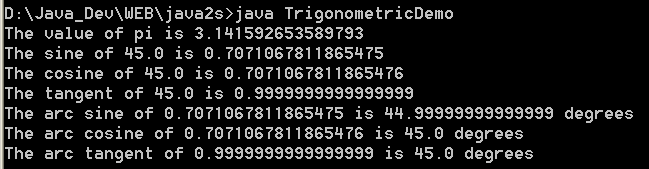 |
| 35. | Complex Number Demo | | |
| 36. | sqrt(a^2 + b^2) without under/overflow | | |
| 37. | Returns an integer hash code representing the given double array value. | | |
| 38. | Returns an integer hash code representing the given double value. | | |
| 39. | Returns n!. Shorthand for n Factorial, the product of the numbers 1,...,n as a double. | | |
| 40. | Returns n!. Shorthand for n Factorial, the product of the numbers 1,...,n. | | |
| 41. | Returns the hyperbolic sine of x. | | |
| 42. | For a double precision value x, this method returns +1.0 if x >= 0 and -1.0 if x < 0. Returns NaN if x is NaN. | | |
| 43. | For a float value x, this method returns +1.0F if x >= 0 and -1.0F if x < 0. Returns NaN if x is NaN. | | |
| 44. | Normalize an angle in a 2&pi wide interval around a center value. | | |
| 45. | Normalizes an angle to a relative angle. | | |
| 46. | Normalizes an angle to an absolute angle | | |
| 47. | Normalizes an angle to be near an absolute angle | | |
| 48. | Returns the natural logarithm of n!. | | |
| 49. | Returns the least common multiple between two integer values. | | |
| 50. | Gets the greatest common divisor of the absolute value of two numbers | | |
| 51. | Matrix manipulation | | |
| 52. | Returns exact (http://mathworld.wolfram.com/BinomialCoefficient.html) Binomial Coefficient | | |
| 53. | Returns a double representation of the (http://mathworld.wolfram.com/BinomialCoefficient.html) Binomial Coefficient | | |
| 54. | Returns the natural log of the (http://mathworld.wolfram.com/BinomialCoefficient.html) Binomial Coefficient | | |
| 55. | Returns the hyperbolic cosine of x. | | |
| 56. | Math Utils | | |
| 57. | Implements the methods which are in the standard J2SE's Math class, but are not in in J2ME's. | | |
| 58. | Utility methods for mathematical problems. | | |
| 59. | A math utility class with static methods. | | |
| 60. | Computes the binomial coefficient "n over k" | | |
| 61. | Log Gamma | | |
| 62. | Log Beta | | |
| 63. | Beta | | |
| 64. | Gamma | | |
| 65. | Factorial | | |
| 66. | Computes p(x;n,p) where x~B(n,p) | | |
| 67. | Returns the sum of two doubles expressed in log space | | |
| 68. | sigmod | | |
| 69. | sigmod rev | | |
| 70. | Numbers that are closer than this are considered equal | | |
| 71. | Returns the KL divergence, K(p1 || p2). | | |
| 72. | Returns the sum of two doubles expressed in log space | | |
| 73. | Returns the difference of two doubles expressed in log space | | |
| 74. | Is Prime | | |
| 75. | Statistical functions on arrays of numbers, namely, the mean, variance, standard deviation, covariance, min and max | | |
| 76. | This class calculates the Factorial of a numbers passed into the program through command line arguments. | |  |
| 77. | Calculates the Greatest Common Divisor of two numbers passed into the program through command line arguments. | | |
| 78. | Variance: the square of the standard deviation. | | |
| 79. | Population Standard Deviation | | |
| 80. | Returns from a static prime table the least prime that is greater than or equal to a specified value. | | |