Computes p(x;n,p) where x~B(n,p) : Math « Development Class « Java

1. Java
2. Development Class
3. Math

Computes p(x;n,p) where x~B(n,p)

      
/* Copyright (C) 2003 Univ. of Massachusetts Amherst, Computer Science Dept.
   This file is part of "MALLET" (MAchine Learning for LanguagE Toolkit).
   http://www.cs.umass.edu/~mccallum/mallet
   This software is provided under the terms of the Common Public License,
   version 1.0, as published by http://www.opensource.org.  For further
   information, see the file `LICENSE' included with this distribution. */

//package cc.mallet.util;


/**
 * 
 * 
 * @author <a href="mailto:casutton@cs.umass.edu">Charles Sutton</a>
 * @version $Id: ArrayUtils.java,v 1.1 2007/10/22 21:37:40 mccallum Exp $
 */
public class Util {

    /**
     * Computes p(x;n,p) where x~B(n,p)
     */
    // Copied as the "classic" method from Catherine Loader.
    //  Fast and Accurate Computation of Binomial Probabilities.
    //   2001.  (This is not the fast and accurate version.)
    public static double logBinom (int x, int n, double p)
    {
      return logFactorial (n) - logFactorial (x) - logFactorial (n - x)
              + (x*Math.log (p)) + ((n-x)*Math.log (1-p));
    }
    public static double logFactorial (int n) {
        return logGamma(n+1);
      }

  // From libbow, dirichlet.c
  // Written by Tom Minka <minka@stat.cmu.edu>
  public static final double logGamma (double x)
  {
    double result, y, xnum, xden;
    int i;
    final double d1 = -5.772156649015328605195174e-1;
    final double p1[] = { 
      4.945235359296727046734888e0, 2.018112620856775083915565e2, 
      2.290838373831346393026739e3, 1.131967205903380828685045e4, 
      2.855724635671635335736389e4, 3.848496228443793359990269e4, 
      2.637748787624195437963534e4, 7.225813979700288197698961e3 
    };
    final double q1[] = {
      6.748212550303777196073036e1, 1.113332393857199323513008e3, 
      7.738757056935398733233834e3, 2.763987074403340708898585e4, 
      5.499310206226157329794414e4, 6.161122180066002127833352e4, 
      3.635127591501940507276287e4, 8.785536302431013170870835e3
    };
    final double d2 = 4.227843350984671393993777e-1;
    final double p2[] = {
      4.974607845568932035012064e0, 5.424138599891070494101986e2, 
      1.550693864978364947665077e4, 1.847932904445632425417223e5, 
      1.088204769468828767498470e6, 3.338152967987029735917223e6, 
      5.106661678927352456275255e6, 3.074109054850539556250927e6
    };
    final double q2[] = {
      1.830328399370592604055942e2, 7.765049321445005871323047e3, 
      1.331903827966074194402448e5, 1.136705821321969608938755e6, 
      5.267964117437946917577538e6, 1.346701454311101692290052e7, 
      1.782736530353274213975932e7, 9.533095591844353613395747e6
    };
    final double d4 = 1.791759469228055000094023e0;
    final double p4[] = {
      1.474502166059939948905062e4, 2.426813369486704502836312e6, 
      1.214755574045093227939592e8, 2.663432449630976949898078e9, 
      2.940378956634553899906876e10, 1.702665737765398868392998e11, 
      4.926125793377430887588120e11, 5.606251856223951465078242e11
    };
    final double q4[] = {
      2.690530175870899333379843e3, 6.393885654300092398984238e5, 
      4.135599930241388052042842e7, 1.120872109616147941376570e9, 
      1.488613728678813811542398e10, 1.016803586272438228077304e11, 
      3.417476345507377132798597e11, 4.463158187419713286462081e11
    };
    final double c[] = {
      -1.910444077728e-03, 8.4171387781295e-04, 
      -5.952379913043012e-04, 7.93650793500350248e-04, 
      -2.777777777777681622553e-03, 8.333333333333333331554247e-02, 
      5.7083835261e-03
    };
    final double a = 0.6796875;

    if((x <= 0.5) || ((x > a) && (x <= 1.5))) {
      if(x <= 0.5) {
        result = -Math.log(x);
        /*  Test whether X < machine epsilon. */
        if(x+1 == 1) {
          return result;
        }
      }
      else {
        result = 0;
        x = (x - 0.5) - 0.5;
      }
      xnum = 0;
      xden = 1;
      for(i=0;i<8;i++) {
        xnum = xnum * x + p1[i];
        xden = xden * x + q1[i];
      }
      result += x*(d1 + x*(xnum/xden));
    }
    else if((x <= a) || ((x > 1.5) && (x <= 4))) {
      if(x <= a) {
        result = -Math.log(x);
        x = (x - 0.5) - 0.5;
      }
      else {
        result = 0;
        x -= 2;
      }
      xnum = 0;
      xden = 1;
      for(i=0;i<8;i++) {
        xnum = xnum * x + p2[i];
        xden = xden * x + q2[i];
      }
      result += x*(d2 + x*(xnum/xden));
    }
    else if(x <= 12) {
      x -= 4;
      xnum = 0;
      xden = -1;
      for(i=0;i<8;i++) {
        xnum = xnum * x + p4[i];
        xden = xden * x + q4[i];
      }
      result = d4 + x*(xnum/xden);
    }
    /*  X > 12  */
    else {
      y = Math.log(x);
      result = x*(y - 1) - y*0.5 + .9189385332046727417803297;
      x = 1/x;
      y = x*x;
      xnum = c[6];
      for(i=0;i<6;i++) {
        xnum = xnum * y + c[i];
      }
      xnum *= x;
      result += xnum;
    }
    return result;
  }
  
}

   
    
    
    
    
    
  

Related examples in the same category

1.	Absolute value
2.	Find absolute value of float, int, double and long using Math.abs
3.	Find ceiling value of a number using Math.ceil
4.	Find exponential value of a number using Math.exp
5.	Find floor value of a number using Math.floor
6.	Find minimum of two numbers using Math.min
7.	Find power using Math.pow
8.	Find square root of a number using Math.sqrt
9.	Find natural logarithm value of a number using Math.log
10.	Find maximum of two numbers using Math.max
11.	Get the power value
12.	Using the Math Trig Methods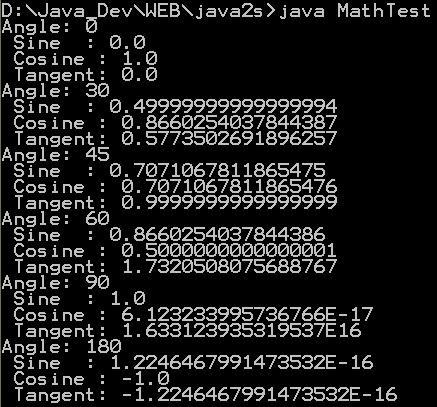
13.	Using BigDecimal for Precision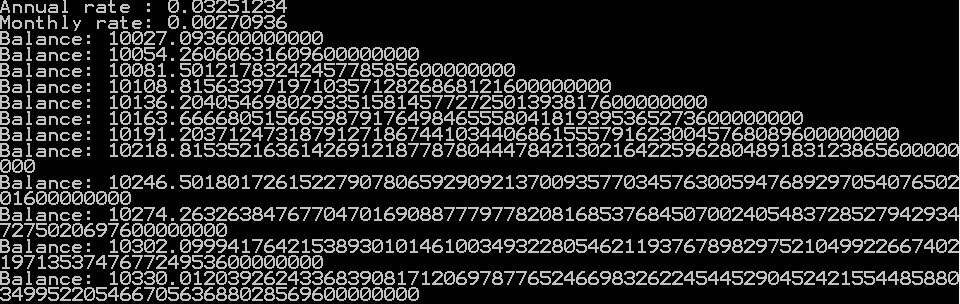
14.	Demonstrate our own version round()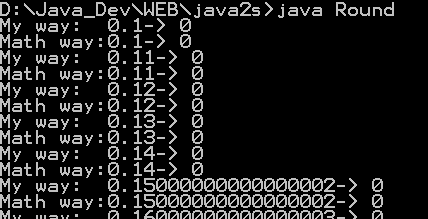
15.	Demonstrate a few of the Math functions for Trigonometry
16.	Exponential Demo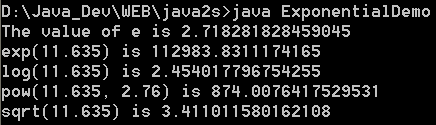
17.	Min Demo
18.	Basic Math Demo
19.	Using strict math in applications
20.	Conversion between polar and rectangular coordinates
21.	Using the pow() function
22.	Using strict math at the method level
23.	Calculating hyperbolic functions
24.	Calculating trigonometric functions
25.	Weighted floating-point comparisons
26.	Solving right triangles
27.	Applying the quadratic formula
28.	Calculate the floor of the log, base 2
29.	Greatest Common Divisor (GCD) of positive integer numbers
30.	Least Common Multiple (LCM) of two strictly positive integer numbers
31.	Moving Average
32.	Make Exponention
33.	Caclulate the factorial of N
34.	Trigonometric Demo
35.	Complex Number Demo
36.	sqrt(a^2 + b^2) without under/overflow
37.	Returns an integer hash code representing the given double array value.
38.	Returns an integer hash code representing the given double value.
39.	Returns n!. Shorthand for n Factorial, the product of the numbers 1,...,n as a double.
40.	Returns n!. Shorthand for n Factorial, the product of the numbers 1,...,n.
41.	Returns the hyperbolic sine of x.
42.	Contains static definition for matrix math methods.
43.	For a double precision value x, this method returns +1.0 if x >= 0 and -1.0 if x < 0. Returns NaN if x is NaN.
44.	For a float value x, this method returns +1.0F if x >= 0 and -1.0F if x < 0. Returns NaN if x is NaN.
45.	Normalize an angle in a 2&pi wide interval around a center value.
46.	Normalizes an angle to a relative angle.
47.	Normalizes an angle to an absolute angle
48.	Normalizes an angle to be near an absolute angle
49.	Returns the natural logarithm of n!.
50.	Returns the least common multiple between two integer values.
51.	Gets the greatest common divisor of the absolute value of two numbers
52.	Matrix manipulation
53.	Returns exact (http://mathworld.wolfram.com/BinomialCoefficient.html) Binomial Coefficient
54.	Returns a double representation of the (http://mathworld.wolfram.com/BinomialCoefficient.html) Binomial Coefficient
55.	Returns the natural log of the (http://mathworld.wolfram.com/BinomialCoefficient.html) Binomial Coefficient
56.	Returns the hyperbolic cosine of x.
57.	Math Utils
58.	Implements the methods which are in the standard J2SE's Math class, but are not in in J2ME's.
59.	Utility methods for mathematical problems.
60.	A math utility class with static methods.
61.	Computes the binomial coefficient "n over k"
62.	Log Gamma
63.	Log Beta
64.	Beta
65.	Gamma
66.	Factorial
67.	Returns the sum of two doubles expressed in log space
68.	sigmod
69.	sigmod rev
70.	Numbers that are closer than this are considered equal
71.	Returns the KL divergence, K(p1 || p2).
72.	Returns the sum of two doubles expressed in log space
73.	Returns the difference of two doubles expressed in log space
74.	Is Prime
75.	Statistical functions on arrays of numbers, namely, the mean, variance, standard deviation, covariance, min and max
76.	This class calculates the Factorial of a numbers passed into the program through command line arguments.
77.	Calculates the Greatest Common Divisor of two numbers passed into the program through command line arguments.
78.	Variance: the square of the standard deviation.
79.	Population Standard Deviation
80.	Returns from a static prime table the least prime that is greater than or equal to a specified value.