Complex Number Demo : Math « Development Class « Java

1. Java
2. Development Class
3. Math

Complex Number Demo

         
/*
3.0+5.0i
3.0+5.0i.getReal() = 3.0
3.0+5.0i + 2.0-2.0i = 5.0+3.0i
3.0+5.0i + 2.0-2.0i = 5.0+3.0i
3.0+5.0i * 2.0-2.0i = 16.0+4.0i
-0.5+2.0i

*/





/** A class to test Complex Numbers. 
 * @author Ian F. Darwin, http://www.darwinsys.com/
 * @version $Id: ComplexDemo.java,v 1.6 2004/05/13 22:28:59 ian Exp $
 */
public class ComplexDemo {
  /** The program */
  public static void main(String[] args) {
    Complex c = new Complex(3,  5);
    Complex d = new Complex(2, -2);
    System.out.println(c);
    System.out.println(c + ".getReal() = " + c.getReal());
    System.out.println(c + " + " + d + " = " + c.add(d));
    System.out.println(c + " + " + d + " = " + Complex.add(c, d));
    System.out.println(c + " * " + d + " = " + c.multiply(d));
    System.out.println(Complex.divide(c, d));
  }
}


/** A class to represent Complex Numbers. A Complex object is
 * immutable once created; the add, subtract and multiply routines
 * return newly-created Complex objects containing the results.
 *
 * @author Ian F. Darwin, inspired by David Flanagan.
 * @version $Id: Complex.java,v 1.3 2004/05/13 22:28:59 ian Exp $
 */
class Complex {
  /** The real part */
  private double r;
  /** The imaginary part */
  private double i;

  /** Construct a Complex */
  Complex(double rr, double ii) {
    r = rr;
    i = ii;
  }

  /** Display the current Complex as a String, for use in
   * println() and elsewhere.
   */
  public String toString() {
    StringBuffer sb = new StringBuffer().append(r);
    if (i>0)
      sb.append('+'); // else append(i) appends - sign
    return sb.append(i).append('i').toString();
  }

  /** Return just the Real part */
  public double getReal() {
    return r;
  }
  /** Return just the Real part */
  public double getImaginary() {
    return i;
  }
  /** Return the magnitude of a complex number */
  public double magnitude() {
    return Math.sqrt(r*r + i*i);
  }

  /** Add another Complex to this one
   */
  public Complex add(Complex other) {
    return add(this, other);
  }

  /** Add two Complexes
   */
  public static Complex add(Complex c1, Complex c2) {
    return new Complex(c1.r+c2.r, c1.i+c2.i);
  }

  /** Subtract another Complex from this one
   */
  public Complex subtract(Complex other) {
    return subtract(this, other);
  }

  /** Subtract two Complexes
   */
  public static Complex subtract(Complex c1, Complex c2) {
    return new Complex(c1.r-c2.r, c1.i-c2.i);
  }

  /** Multiply this Complex times another one
   */
  public Complex multiply(Complex other) {
    return multiply(this, other);
  }

  /** Multiply two Complexes
   */
  public static Complex multiply(Complex c1, Complex c2) {
    return new Complex(c1.r*c2.r - c1.i*c2.i, c1.r*c2.i + c1.i*c2.r);
  }

  /** Divide c1 by c2.
   * @author Gisbert Selke.
   */
  public static Complex divide(Complex c1, Complex c2) {
    return new Complex(
      (c1.r*c2.r+c1.i*c2.i)/(c2.r*c2.r+c2.i*c2.i),
      (c1.i*c2.r-c1.r*c2.i)/(c2.r*c2.r+c2.i*c2.i));
  }
  
  /* Compare this Complex number with another
   */
  public boolean equals(Object o) {
    if (!(o instanceof Complex))
      throw new IllegalArgumentException(
          "Complex.equals argument must be a Complex");
    Complex other = (Complex)o;
    return r == other.r && i == other.i;
  }
  
  /* Generate a hashCode; not sure how well distributed these are.
   */
  public int hashCode() {
    return (int)( r) |  (int)i;
  }
}


           
         
    
    
    
    
    
    
    
    
  

Related examples in the same category

1.	Absolute value
2.	Find absolute value of float, int, double and long using Math.abs
3.	Find ceiling value of a number using Math.ceil
4.	Find exponential value of a number using Math.exp
5.	Find floor value of a number using Math.floor
6.	Find minimum of two numbers using Math.min
7.	Find power using Math.pow
8.	Find square root of a number using Math.sqrt
9.	Find natural logarithm value of a number using Math.log
10.	Find maximum of two numbers using Math.max
11.	Get the power value
12.	Using the Math Trig Methods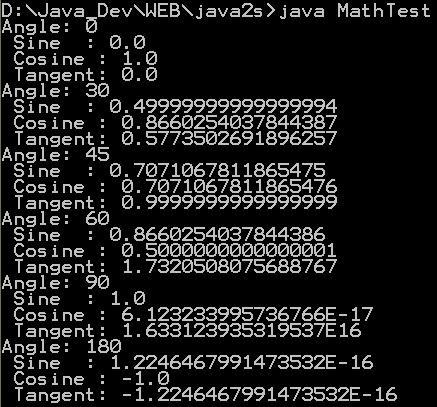
13.	Using BigDecimal for Precision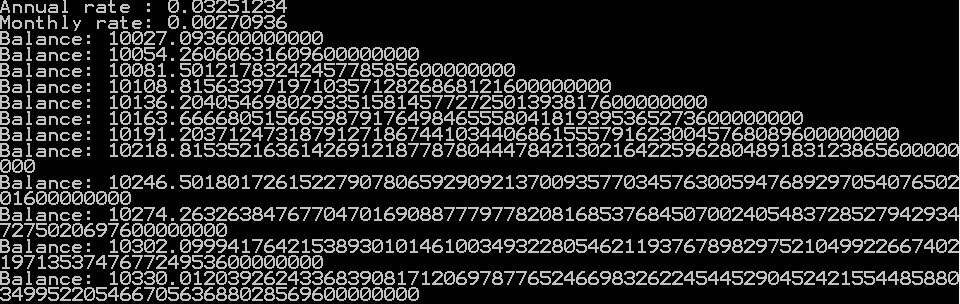
14.	Demonstrate our own version round()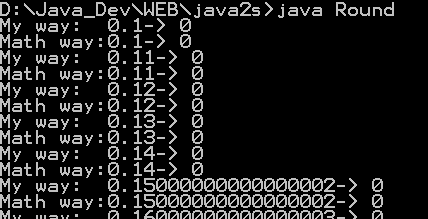
15.	Demonstrate a few of the Math functions for Trigonometry
16.	Exponential Demo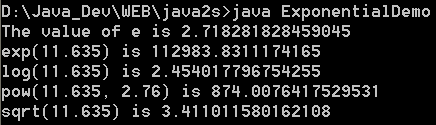
17.	Min Demo
18.	Basic Math Demo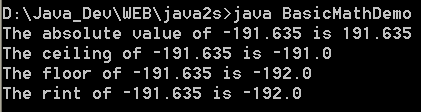
19.	Using strict math in applications
20.	Conversion between polar and rectangular coordinates
21.	Using the pow() function
22.	Using strict math at the method level
23.	Calculating hyperbolic functions
24.	Calculating trigonometric functions
25.	Weighted floating-point comparisons
26.	Solving right triangles
27.	Applying the quadratic formula
28.	Calculate the floor of the log, base 2
29.	Greatest Common Divisor (GCD) of positive integer numbers
30.	Least Common Multiple (LCM) of two strictly positive integer numbers
31.	Moving Average
32.	Make Exponention
33.	Caclulate the factorial of N
34.	Trigonometric Demo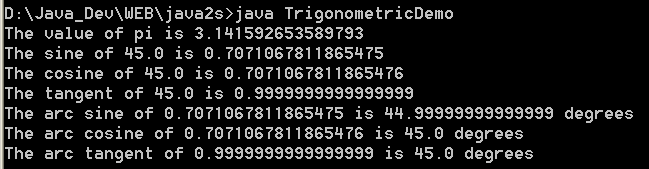
35.	sqrt(a^2 + b^2) without under/overflow
36.	Returns an integer hash code representing the given double array value.
37.	Returns an integer hash code representing the given double value.
38.	Returns n!. Shorthand for n Factorial, the product of the numbers 1,...,n as a double.
39.	Returns n!. Shorthand for n Factorial, the product of the numbers 1,...,n.
40.	Returns the hyperbolic sine of x.
41.	Contains static definition for matrix math methods.
42.	For a double precision value x, this method returns +1.0 if x >= 0 and -1.0 if x < 0. Returns NaN if x is NaN.
43.	For a float value x, this method returns +1.0F if x >= 0 and -1.0F if x < 0. Returns NaN if x is NaN.
44.	Normalize an angle in a 2&pi wide interval around a center value.
45.	Normalizes an angle to a relative angle.
46.	Normalizes an angle to an absolute angle
47.	Normalizes an angle to be near an absolute angle
48.	Returns the natural logarithm of n!.
49.	Returns the least common multiple between two integer values.
50.	Gets the greatest common divisor of the absolute value of two numbers
51.	Matrix manipulation
52.	Returns exact (http://mathworld.wolfram.com/BinomialCoefficient.html) Binomial Coefficient
53.	Returns a double representation of the (http://mathworld.wolfram.com/BinomialCoefficient.html) Binomial Coefficient
54.	Returns the natural log of the (http://mathworld.wolfram.com/BinomialCoefficient.html) Binomial Coefficient
55.	Returns the hyperbolic cosine of x.
56.	Math Utils
57.	Implements the methods which are in the standard J2SE's Math class, but are not in in J2ME's.
58.	Utility methods for mathematical problems.
59.	A math utility class with static methods.
60.	Computes the binomial coefficient "n over k"
61.	Log Gamma
62.	Log Beta
63.	Beta
64.	Gamma
65.	Factorial
66.	Computes p(x;n,p) where x~B(n,p)
67.	Returns the sum of two doubles expressed in log space
68.	sigmod
69.	sigmod rev
70.	Numbers that are closer than this are considered equal
71.	Returns the KL divergence, K(p1 || p2).
72.	Returns the sum of two doubles expressed in log space
73.	Returns the difference of two doubles expressed in log space
74.	Is Prime
75.	Statistical functions on arrays of numbers, namely, the mean, variance, standard deviation, covariance, min and max
76.	This class calculates the Factorial of a numbers passed into the program through command line arguments.
77.	Calculates the Greatest Common Divisor of two numbers passed into the program through command line arguments.
78.	Variance: the square of the standard deviation.
79.	Population Standard Deviation
80.	Returns from a static prime table the least prime that is greater than or equal to a specified value.