A Complex Number Class : Complex « Data Types « C# / C Sharp

1. C# / C Sharp
2. Data Types
3. Complex

A Complex Number Class

  
/*
A Programmer's Introduction to C# (Second Edition)
by Eric Gunnerson

Publisher: Apress  L.P.
ISBN: 1-893115-62-3
*/
// 25 - Operator Overloading\A Complex Number Class
// copyright 2000 Eric Gunnerson
using System;

struct Complex
{
    float real;
    float imaginary;
    
    public Complex(float real, float imaginary)
    {
        this.real = real;
        this.imaginary = imaginary;
    }
    
    public float Real
    {
        get
        {
            return(real);
        }
        set
        {
            real = value;
        }
    }
    
    public float Imaginary
    {
        get
        {
            return(imaginary);
        }
        set
        {
            imaginary = value;
        }
    }
    
    public override string ToString()
    {
        return(String.Format("({0}, {1}i)", real, imaginary));
    }
    
    public static bool operator==(Complex c1, Complex c2)
    {
        if ((c1.real == c2.real) &&
        (c1.imaginary == c2.imaginary))
        return(true);
        else
        return(false);
    }
    
    public static bool operator!=(Complex c1, Complex c2)
    {
        return(!(c1 == c2));
    }
    
    public override bool Equals(object o2)
    {
        Complex c2 = (Complex) o2;
        
        return(this == c2);
    }
    
    public override int GetHashCode()
    {
        return(real.GetHashCode() ^ imaginary.GetHashCode());
    }
    
    public static Complex operator+(Complex c1, Complex c2)
    {
        return(new Complex(c1.real + c2.real, c1.imaginary + c2.imaginary));
    }
    
    public static Complex operator-(Complex c1, Complex c2)
    {
        return(new Complex(c1.real - c2.real, c1.imaginary - c2.imaginary));
    }
    
    // product of two complex numbers
    public static Complex operator*(Complex c1, Complex c2)
    {
        return(new Complex(c1.real * c2.real - c1.imaginary * c2.imaginary,
        c1.real * c2.imaginary + c2.real * c1.imaginary));
    }
    
    // quotient of two complex numbers
    public static Complex operator/(Complex c1, Complex c2)
    {
        if ((c2.real == 0.0f) &&
        (c2.imaginary == 0.0f))
        throw new DivideByZeroException("Can't divide by zero Complex number");
        
        float newReal = 
        (c1.real * c2.real + c1.imaginary * c2.imaginary) /
        (c2.real * c2.real + c2.imaginary * c2.imaginary);
        float newImaginary = 
        (c2.real * c1.imaginary - c1.real * c2.imaginary) /
        (c2.real * c2.real + c2.imaginary * c2.imaginary);
        
        return(new Complex(newReal, newImaginary));
    }
    
    // non-operator versions for other languages
    public static Complex Add(Complex c1, Complex c2)
    {
        return(c1 + c2);
    }
    
    public static Complex Subtract(Complex c1, Complex c2)
    {
        return(c1 - c2);
    }
    
    public static Complex Multiply(Complex c1, Complex c2)
    {
        return(c1 * c2);
    }
    
    public static Complex Divide(Complex c1, Complex c2)
    {
        return(c1 / c2);
    }
}

public class AComplexNumberClass
{
    public static void Main()
    {
        Complex c1 = new Complex(3, 1);
        Complex c2 = new Complex(1, 2);
        
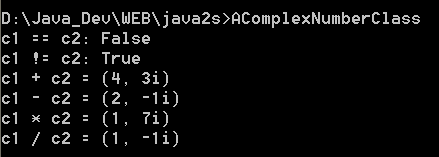
        Console.WriteLine("c1 == c2: {0}", c1 == c2);
        Console.WriteLine("c1 != c2: {0}", c1 != c2);
        Console.WriteLine("c1 + c2 = {0}", c1 + c2);
        Console.WriteLine("c1 - c2 = {0}", c1 - c2);
        Console.WriteLine("c1 * c2 = {0}", c1 * c2);
        Console.WriteLine("c1 / c2 = {0}", c1 / c2);
    }
}

           
         
    
  

Related examples in the same category